Sparx Sharpener: Worth the Money?
I’ve recently seen a few of the hockey personalities that I follow on YouTube mention the Sparx skate sharpener. At $799.99 for the base sharpener (but closer to $1,600 once you actually look at the numbers), it seems like a pretty good deal - with a few caveats.
Personally, I hate going to the shop to get my skates sharpened. I work during the day, and I’m usually not thinking about my skates until after the shop has closed. I also skate multiple times per week - I play in two or three beer leagues, I coach a youth team that practices two or three times a week, and I’m planning to ref starting next year - so I have to get my skates sharpened about every other week. It’s a pain in the butt, so the Sparx sharpener seemed like it might be a good option.
Once I ran the numbers (see below for the assumptions that I made), I came to the conclusion that I would break even after 220 sharpenings - on April 19, 2026. Keep reading for a more detailed explanation - and some pretty graphs! - of how I came to that conclusion. I also consider other scenarios where it may or may not make sense to buy the Sparx.
Assumption 1: Cost
Let’s go super basic - even fewer accessories than the “basic bundle” they seem to recommend. (The prices are from today, January 30, 2022.)
- Sparx Sharpener: $799.99
- Edge Checker: $139.99
- Deburring Block Set: $44.99
- Grinding Ring Starter Set: $164.99
That’s $1,149.96 before tax and shipping. A quick esimation for taxes and shipping on their website yields the following.
- Estimated Tax (~8%): $92.00
- Estimated Shipping: $35.00
That brings total spend to $1,276.96.
Assumption 2: Sharpenings Per Ring
The original set of rings advertised 40 sharpenings per ring (at $39.99). However, after multiple price hikes (to $64.99), the number of sharpenings was increased to 60 (with no change in hardware). The theory is that they collected data over a large amount of at-home consumers and concluded that those consumers largely ended up doing fewer passes per sharpening, which allowed them to put a higher number of sharpenings on the box. For a transparent, data-based retrospective, I suggest you watch this YouTube video from “Seen By Yosh,” where he summarizes the longitudinal data he collected. Based on his findings, I’m going to split the difference and assume 50 sharpenings per ring.
Assumption 3: Cost Per Sharpening
I get my skates sharpened at Pure Hockey (notably often at the locations that use a Sparx sharpener behind the scenes), where it costs $7.00 per sharpening. Thus, I’m going to use that for my assumed cost per sharpening.
Assumption 4: Sharpening Frequency
I play three times per week in a beer league setting. We usually skate four defenders, so I usually end up skating about half the game. I also coach two to three on-ice practices per week, but it’s a lot of standing and running drills rather than actual skating, of course. Though I currently get my skates sharpened every other week, I’m going to assume that I’ll sharpen once per week (with less material removed) if I get the Sparx sharpener.
Assumption Summary
At this point, I’ve made the following assumptions:
- Total Spend: $1,276.96
- Sharpenings Per Ring: 50
- Cost Per Sharpenings: $7.00
- Sharpenings Per Week: 1
Napkin Math Method
Calculating the number of sharpenings it would take to break even could be a pretty simple calculation, right? It should be the total spend divided by the cost of getting your skates sharpened elsewhere. With a total spend of $1,276.96 and $7.00 per sharpening, that comes out to 182.42 sharpenings, which I’ll round up to 183 sharpenings.
However, that’s more than the one sharpening ring I priced out (since I always use the same hollow). Because I’m assuming that each ring can do 50 sharpenings, I’ll need 4 rings total. I already bought 1 when I bought the starter pack, so I’ll have to buy 3 more. That brings my new total spend to $1,471.93 and my new break-even sharpening count to 211.
But that doesn’t fit in the 4 rings that I have, so I’d better buy 1 more! I’ve now spent $1,536.92, so I’ll break even after 220 sharpenings - on April 19, 2026.
However, there’s a huge drawback to this method - namely that it took a good bit of manual calculation (since we had to add rings a few times) to come to this conclusion. Instead, let’s generate the data! It takes care of this drawback (and it’s way more fun).
In summary…
The “Napkin Math” method tells me that I’ll break even after 220 sharpenings (on April 19, 2026), but there’s an issue with the approach.
Data Generation Method
Let’s generate 500 data points as a great starting point. That’s a lot of sharpenings! (I also assumed that I’d be buying the rings as I went, so I’ve reset the initial total spend.)
Here’s the R code:
# Restate assumptions
pub_date <- as.Date("2022-01-30")
total_spend <- sum(c(799.99, 139.99, 44.99, 164.99, 92.00, 35.00))
sharpenings_per_ring <- 50
cost_per_ring <- 64.99
cost_per_sharpening <- 7
sharpenings_per_week <- 1.0
# Build data table
df_sharp <- data.frame(pub_date + (cost_per_sharpening / sharpenings_per_week) * 1:500, rep(cost_per_sharpening, 500), cost_per_sharpening * 1:500)
names(df_sharp) <- c("Date", "Pure Hockey Cost Per", "Pure Hockey Cumulative")
df_sharp$`Sparx Cost Per` <- (total_spend + floor(seq.int(nrow(df_sharp)) / sharpenings_per_ring) * cost_per_ring) / 1:500
df_sharp$`Sparx Cumulative` <- total_spend + floor(seq.int(nrow(df_sharp)) / sharpenings_per_ring) * cost_per_ring
# Calculate break even point
break_even_sharpenings <- min(which(df_sharp$`Sparx Cumulative` < df_sharp$`Pure Hockey Cumulative`))
break_even_date <- pub_date + break_even_sharpenings * (7 / sharpenings_per_week)
# Build formatted data table
df_sharp_formatted <- df_sharp
df_sharp_formatted$`Pure Hockey Cost Per` %<>% sapply(scales::dollar_format(accuracy = .01))
df_sharp_formatted$`Pure Hockey Cumulative` %<>% sapply(scales::dollar_format(accuracy = .01))
df_sharp_formatted$`Sparx Cost Per` %<>% sapply(scales::dollar_format(accuracy = .01))
df_sharp_formatted$`Sparx Cumulative` %<>% sapply(scales::dollar_format(accuracy = .01))
# Print formatted data table (first 10 rows)
knitr::kable(head(df_sharp_formatted, 10), align = "r", row.names = TRUE)
# Print formatted data table (at break-even point)
knitr::kable(tail(head(df_sharp_formatted, break_even_sharpenings + 5), 10), align = "r", row.names = TRUE)
Here are the first ten rows.
| Date | PH Each | PH Cumulative | Sparx Each | Sparx Cumulative |
|---|---|---|---|---|
| 2022-02-06 | $7.00 | $7.00 | $1,276.96 | $1,276.96 |
| 2022-02-13 | $7.00 | $14.00 | $638.48 | $1,276.96 |
| 2022-02-20 | $7.00 | $21.00 | $425.65 | $1,276.96 |
| 2022-02-27 | $7.00 | $28.00 | $319.24 | $1,276.96 |
| 2022-03-06 | $7.00 | $35.00 | $255.39 | $1,276.96 |
| 2022-03-13 | $7.00 | $42.00 | $212.83 | $1,276.96 |
| 2022-03-20 | $7.00 | $49.00 | $182.42 | $1,276.96 |
| 2022-03-27 | $7.00 | $56.00 | $159.62 | $1,276.96 |
| 2022-04-03 | $7.00 | $63.00 | $141.88 | $1,276.96 |
| 2022-04-10 | $7.00 | $70.00 | $127.70 | $1,276.96 |
Using that data, I came to the same conclusion that I’ll break even after 220 sharpenings - on April 19, 2026. Here are the rows where the break even switch happens.
| Date | PH Each | PH Cumulative | Sparx Each | Sparx Cumulative |
|---|---|---|---|---|
| 2026-03-22 | $7.00 | $1,512.00 | $7.12 | $1,536.92 |
| 2026-03-29 | $7.00 | $1,519.00 | $7.08 | $1,536.92 |
| 2026-04-05 | $7.00 | $1,526.00 | $7.05 | $1,536.92 |
| 2026-04-12 | $7.00 | $1,533.00 | $7.02 | $1,536.92 |
| 2026-04-19 | $7.00 | $1,540.00 | $6.99 | $1,536.92 |
| 2026-04-26 | $7.00 | $1,547.00 | $6.95 | $1,536.92 |
| 2026-05-03 | $7.00 | $1,554.00 | $6.92 | $1,536.92 |
| 2026-05-10 | $7.00 | $1,561.00 | $6.89 | $1,536.92 |
| 2026-05-17 | $7.00 | $1,568.00 | $6.86 | $1,536.92 |
| 2026-05-24 | $7.00 | $1,575.00 | $6.83 | $1,536.92 |
In summary…
The “Data Generation” method (is more fun and) tells me that I’ll break even after 220 sharpenings (on April 19, 2026). Same conclusion, better approach!
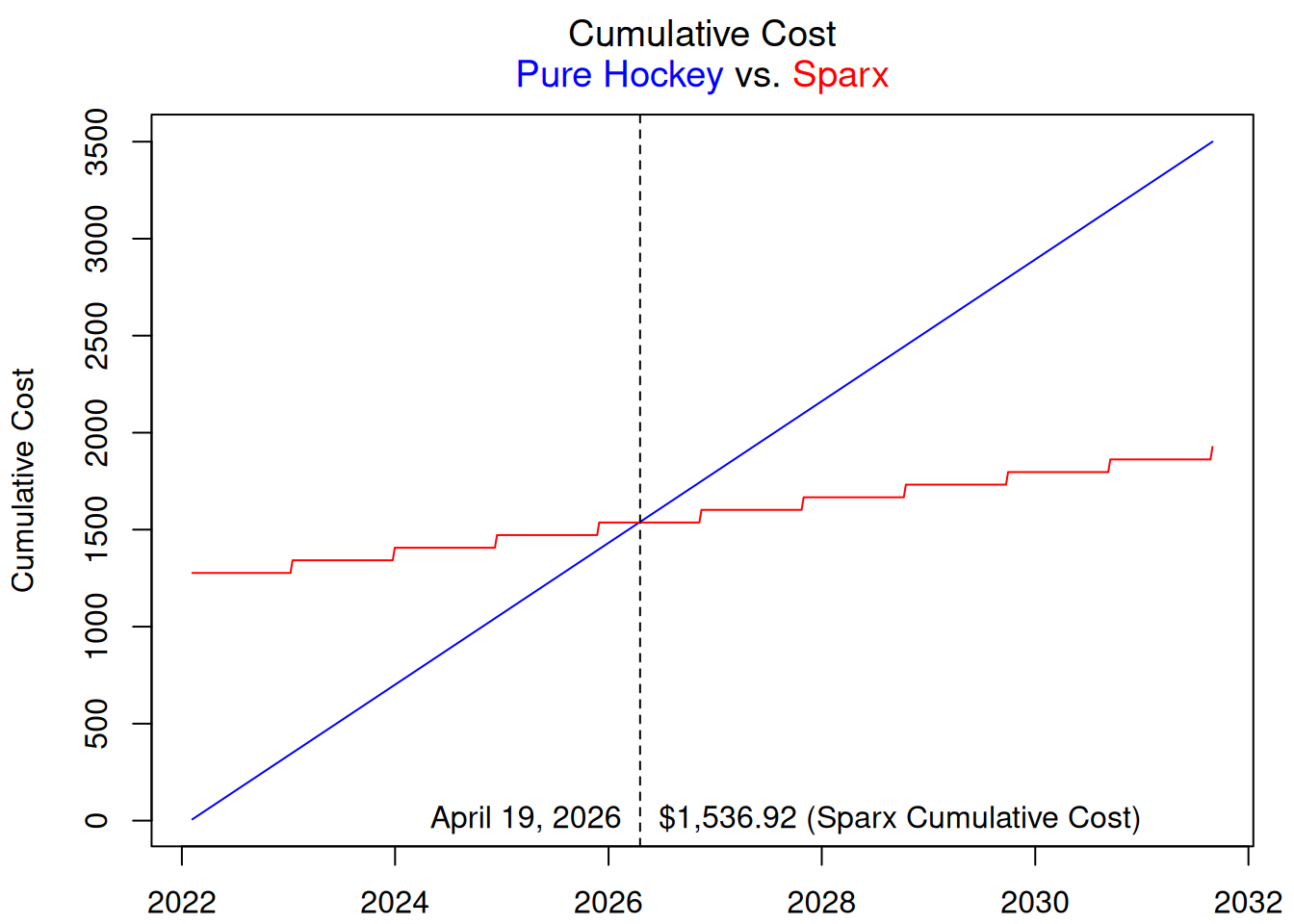
Look at this graph…
Now that I’ve generated data, let’s generate some graphs! First, let’s graph the cumulative cost.
par(mar = c(2.1,4.1,3.1,1.1))
plot(
df_sharp$`Pure Hockey Cumulative` ~ df_sharp$Date, type = "l", col = "blue",
xlab = "", ylab = "Cumulative Cost"
)
lines(df_sharp$`Sparx Cumulative` ~ df_sharp$Date, type = "l", col = "red")
abline(v = break_even_date, lty = 2)
text(
x = break_even_date, y = 0, pos = 2,
format(break_even_date, format = "%B %d, %Y")
)
text(
x = break_even_date, y = 0, pos = 4,
paste0(df_sharp_formatted$`Sparx Cumulative`[which(df_sharp$Date == break_even_date)], " (Sparx Cumulative Cost)")
)
title(expression("Cumulative Cost\n"), col.main = "black", line = 1)
title(expression("Pure Hockey " * phantom("vs. Sparx")), col.main = "blue", line = 1)
title(expression(phantom("Pure Hockey ") * "vs. " * phantom("Sparx")), col.main = "black", line = 1)
title(expression(phantom("Pure Hockey vs. ") * "Sparx"), col.main = "red", line = 1)
This, again, shows that I’ll break even on April 19, 2026 (after 220 sharpenings), as represented by the dashed line.
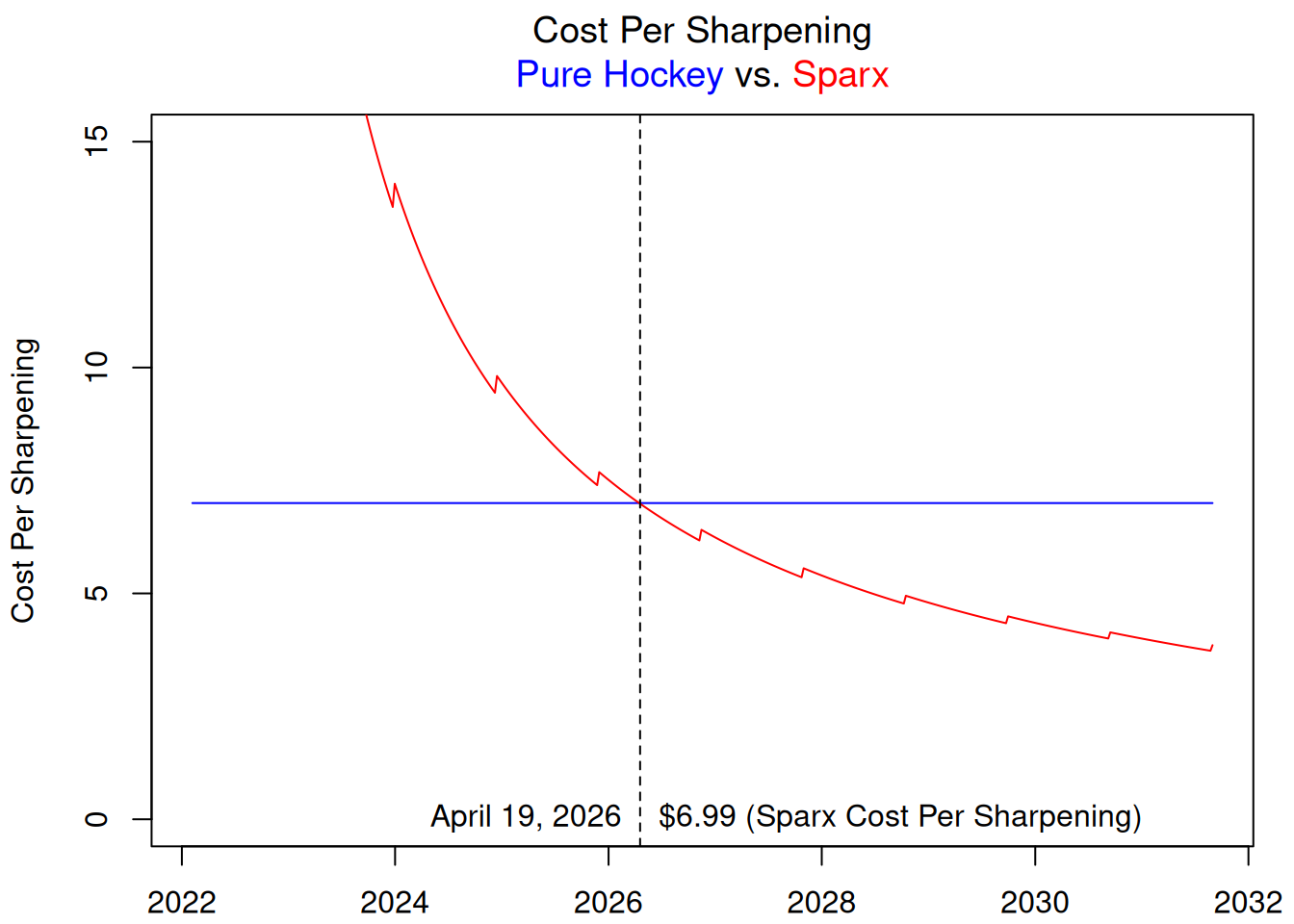
We can create a very similar graph for the cost per sharpening.
par(mar = c(2.1,4.1,3.1,1.1))
plot(
df_sharp$`Pure Hockey Cost Per` ~ df_sharp$Date, type = "l", col = "blue",
xlab = "", ylab = "Cost Per Sharpening", ylim = c(0, 15)
)
lines(df_sharp$`Sparx Cost Per` ~ df_sharp$Date, type = "l", col = "red")
abline(v = break_even_date, lty = 2)
text(
x = break_even_date, y = 0, pos = 2,
format(break_even_date, format = "%B %d, %Y")
)
text(
x = break_even_date, y = 0, pos = 4,
paste0(df_sharp_formatted$`Sparx Cost Per`[which(df_sharp$Date == break_even_date)], " (Sparx Cost Per Sharpening)")
)
title(expression("Cost Per Sharpening\n"), col.main = "black", line = 1)
title(expression("Pure Hockey " * phantom("vs. Sparx")), col.main = "blue", line = 1)
title(expression(phantom("Pure Hockey ") * "vs. " * phantom("Sparx")), col.main = "black", line = 1)
title(expression(phantom("Pure Hockey vs. ") * "Sparx"), col.main = "red", line = 1)
It shows (unsurprisingly) exactly the same conclusion.
Conclusion
At this point, we have a generalized method that we can use to determine when you’ll break even on your Sparx purchase.
rationalizeSparxCount <- function(total_spend, sharpenings_per_ring, cost_per_ring, cost_per_sharpening, sharpenings_per_week, pub_date) {
df_sharp <- data.frame(pub_date + (7 / sharpenings_per_week) * 1:500, rep(cost_per_sharpening, 500), cost_per_sharpening * 1:500)
names(df_sharp) <- c("Date", "Pure Hockey Cost Per", "Pure Hockey Cumulative")
df_sharp$`Sparx Cost Per` <- (total_spend + floor(seq.int(nrow(df_sharp)) / sharpenings_per_ring) * 64.99) / 1:500
df_sharp$`Sparx Cumulative` <- total_spend + floor(seq.int(nrow(df_sharp)) / sharpenings_per_ring) * 64.99
break_even_sharpenings <- min(which(df_sharp$`Sparx Cumulative` < df_sharp$`Pure Hockey Cumulative`))
return(break_even_sharpenings)
}
rationalizeSparxDate <- function(total_spend, sharpenings_per_ring, cost_per_ring, cost_per_sharpening, sharpenings_per_week, pub_date) {
return(pub_date + rationalizeSparxCount(
total_spend = total_spend,
sharpenings_per_ring = sharpenings_per_ring,
cost_per_ring = cost_per_ring,
cost_per_sharpening = cost_per_sharpening,
sharpenings_per_week = sharpenings_per_week,
pub_date = pub_date
) * (7 / sharpenings_per_week))
}
Let’s run through a few different scenarios:
- You’re a 1-skater household, and you skate in beer league once a week. You only sharpen (for $7.00) your skates once every four weeks. You’ll break even on December 12, 2038. Should you buy a Sparx sharpener? No. Absolutely not. I have no idea how long Sparx sharpeners last, but more than 15 years is probably too much to ask.
- You’re a 1-skater household, but you skate many times per week (maybe you’re a ref) and sharpen (for $7.00) your skates once a week. You’ll break even on April 19, 2026. That’s just about four years from now. Should you buy a Sparx sharpener? Maybe. You’ll have to consider the intangibles, which I’ll get to in just a minute.
- You coach your kid’s team. You sharpen your skates once a month and your kid’s skates every week (for $8.00 each). You’ll break even on November 25, 2024. Should you buy a Sparx sharpener? Looks like a good option if you’re confident your kid is going to continue playing for at least a few more years.
- You’re a parent with three kids who all play hockey multiple times per week, so you sharpen each of their skates every week. Unfortunately, you live in a place where skate sharpening is more expensive (let’s say $10.00). You’ll break even on December 25, 2022. Should you buy a Sparx sharpener? Considering you’ll break even within the year, I’d say absolutely.
Did I miss your scenario? If so, you can use the R code above to run it!
Overall, the Sparx sharpener seems like a pretty good deal (when you only consider it from a financial perspective) provided you skate multiple times per week (or have multiple skaters in your household) and therefore sharpen your skates once a week. This qualification that it only really makes sense if you skate multiple time per week or have multiple skaters in your household is obviously very important.
If we exapnd beyond the financial perspective we’ve taken thus far, there are other intangibles to consider for a Sparx sharpener. For example:
- You might now have easy access to high-quality skate sharpening that abounds here in Minnesota.
- You might travel with your skates a lot and want to be able to sharpen them on the road without having to worry about whether the person sharpening them is any good (in which case don’t forget to add the carrying case to your total cost).
- You might not be able to make it to the shop to get your skates sharpened while they open because you work in the day and play hockey in the evening.
- In all of these scenarios, the cost of the Sparx sharpener might be easily overcome by the other problems it solves.
Of course, this should not be a surprising conclusion. Obviously the Sparx sharpener is a better deal the more frequently you use it, and the intangibles are exactly what they use to convince you it’s worth it even if you’re not going to break even quickly.
Stay tuned for the next installments in this analysis. I’ll do a similar analysis where you also monetize your new skate sharpener, and I’ll let you know how I ended up using mine. The former should be out shortly, but don’t expect the latter any time soon as it will take me quite some time to collect the data.